3. 삼각함수, 회전을 위한 수학

회전하면 딱 떠오르는 도형은 원이다. 회전은 원의 궤적을 따라 움직이고 이를 이해하고 구현하기 위해서는

원과 밀접하게 연결되어 있는 삼각함수에 대해서 알아야 한다. 삼각함수의 어떤 특징 때문에 우리는 회전에서 삼각함수를 사용하게 되는 것인가. 

 

1. 삼각비와 삼각함수

삼각비 말그대로 삼각형에서 나타나는 비율을 의미한다. 비율이란 절대적인 크기와 관계 없이 유지 되는 어떠한 비율에 대한 이야기이다.

직각 삼각형에서 대표적인 삼각비에는 sin, cos, tan가 존재한다. 

기준각 θ를 두고 c는 빗변, a는 밑변 b는 높이라 한다. 물론 θ 의 위치에 따라 변 cb의 사잇각이 기준이 되면 이또한 바뀐다.

다음과 같이 정의 된다.

이때 빗변이 1인 직각삼각형을 좌표평면상에 두면 이는 반지름의 길이가 1인 원의 궤적을 따른다.

이때 위의 삼각비에서 c=1이 되기 때문에

sinθ = a, cosθ = b 가 되고 좌표로 (cosθ, sinθ)으로 표시할 수 있다. 또한 피타고라스의 정리를 이용하여

까지 유도할 수 있다.

 

이제 빗변의 길이가 1이 아닌 임의의 스칼라 r로 일반화 시켜보면

반지름 r을 따르는 원의 궤적을 따르는 직각 삼각형의 꼭지점의 벡터는 r ㆍ (cosθ, sinθ) 로 표현 할 수 있다.

2. 삼각함수의 성질

삼각함수는 일정한 주기가 반복되는 함수이다. 회전 또한 원을 따르기 때문에 돌다보면 원점으로 돌아오는 주기성이 특징이다. 이러한 성질 덕분에 우리는 삼각함수를 이용하여 회전을 구현한다.

 

 해당 수식은 v에 대해서 0도 일때를 나타낸다고 보자.

이때 각도를 점점 증가 시키면 아래의 그래프로 해당 각도의 cos 과 sin 값이 대응된다.

90도가 되면 반대가  된다.

계속 각도를 증가 시켜도 결국 같은 원을 따르기 때문에 [-1,1]의 범위에서 반복되게 된다.

cos 함수

sin함수

또한 cos 함수는 우함수, sin은 기함수이기에 

 

가 성립한다.

 

tan 함수의 경우

 

 

같이 표현될 수 있다.

tan 함수

tan함수에서 주의할 점은 분모 cos 이 0이 되는 각도에서는 정의되지 않는다.

 

2. 삼각함수을 이용한 물체의 회전

회전에 있어서 정확히 말하자면 물체를 회전 시킨다 보다는 물체가 있는 공간을 회전 시키는 것이다.

기저벡터를 활용하여 공간을 정의하고 각각의 기저벡터에 회전이 적용된 새로운 벡터를 통해 회전된 공간을 만드는 것이다.

 

앞서 벡터공간에 속한 모든 벡터는 두 기저벡터 e1, e2에 의 선형 결합에 의해서 만들어 질 수 있다.

 

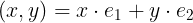
x와 y 를 각각 1이라 했을때 (1,1)의 성분으로 구성된 벡터를 θ만큼 회전 시켜보자.

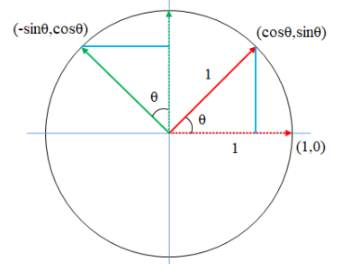
각 기저벡터 e1,e2는

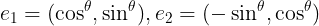
가 된다.

두 벡터의 선형결합을 통해 새로운 벡터를 만들어보자.

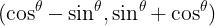
가 되게 된다. 이를 임의의 실수 x, y 로 일반화 하면

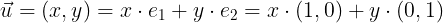
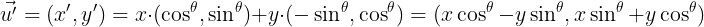
로 일반화 가능하다.